题目
地址:https://leetcode.cn/problems/fibonacci-number/
解题
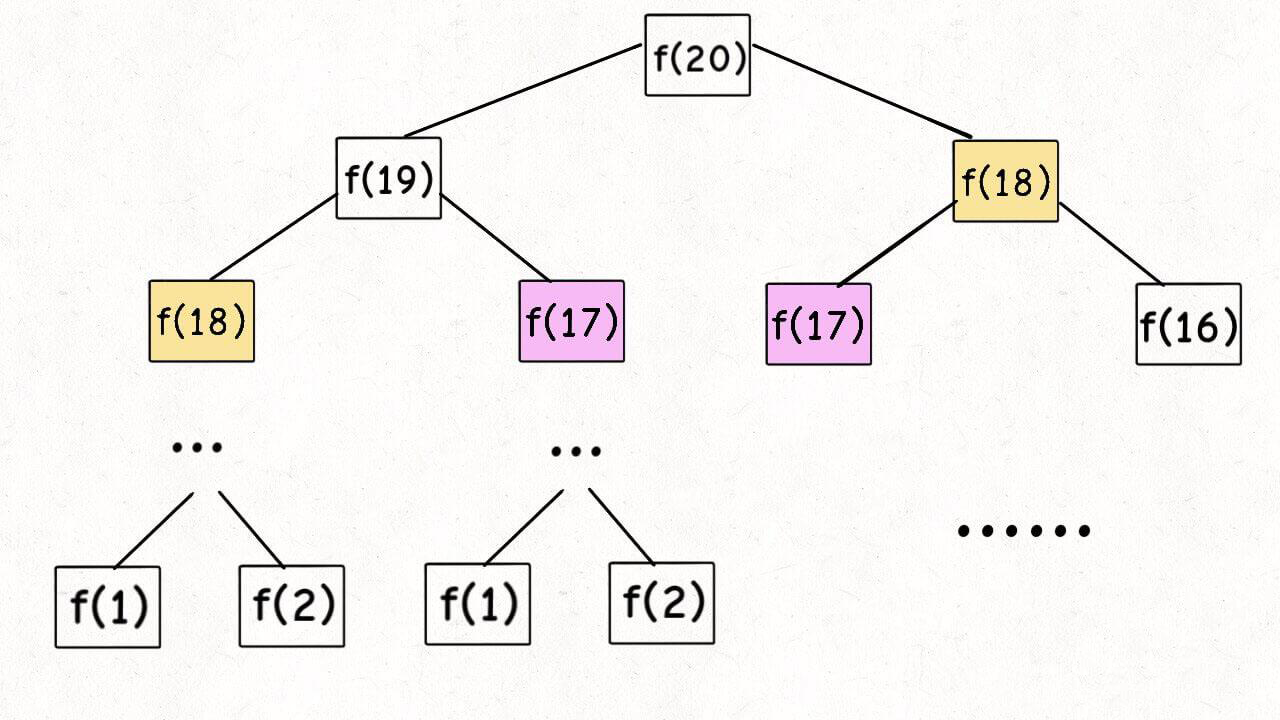
斐波那契数列的特点是由后两个数字相加得出下一个数字, 首先能想到的就是用递归来解决。
递归的出口是
F(0) = 0,F(1) = 1
找到出口之后就很简单了,三下五除二就写出来:
var fib = function (n) {
if (n <= 1) {
return n;
}
function add(num) {
if (num === 1 || num === 0) {
return num;
} else {
return add(num - 1) + add(num - 2);
}
}
return add(n);
};
愉快的提交之后,
嚯,击败了 14% 的提交。
优化
由于盲目的使用递归,造成了大量的重复操作,时间复杂度是 O(2^n),指数级爆炸。
自顶而下
为了解决这些重复的操作,使用 memoization 的思想来对已计算的数据进行缓存。
下面来用 数组 实现一下:
var fib = function (n) {
if (n <= 1) {
return n;
}
let fibArr = [0, 1];
function add(num) {
if (fibArr[num] !== undefined) {
return fibArr[num];
} else {
fibArr[num] = add(num - 1) + add(num - 2);
return fibArr[num];
}
}
return add(n);
};
和之前的简单递归代码相似,不过对未缓存的斐波那契数列进行缓存,再次获取这个数列的时候就从数组中直接取,省去了大量的重复递归操作。
简单的修改之后,再次提交,击败了 92% 的提交,还算可以。
自底向上
上面的解法是自顶而下的求值,还有一种是自底向上的解法。
先计算出需要求的最大值,然后从小到大进行计算。
var fib = function (n) {
if (n <= 1) {
return n;
}
let fibArr = [0, 1];
for (let index = 2; index <= n; index++) {
fibArr[index] = fibArr[index - 1] + fibArr[index - 2];
}
return fibArr[n];
};
不需要使用到递归,或许更好理解。