树
树 是数据结构中很常见的一种数据结构,是一种分层数据的抽象模型。
树形结构存在下列特征:
- 除根节点外,每个节点都有一个父节点
- 每个节点有零个或者多个子节点
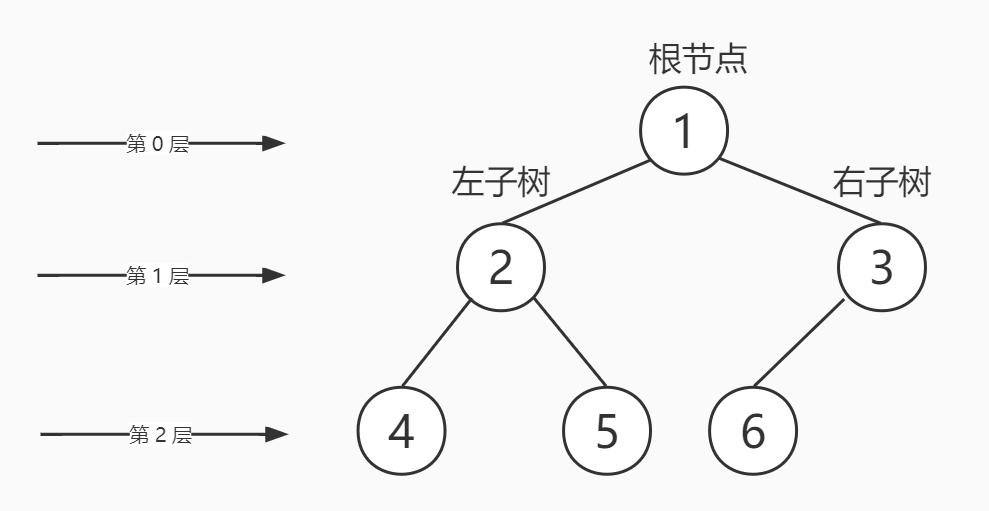
二叉树
二叉树 是树形结构中的一种。 二叉树中的节点最多只能有两个子节点:一个是左节点,一个是右节点。
二叉搜索树(BST)是二叉树的一种,但是只允许你在左节点存储(比父节点)小的值, 在右节点存储(比父节点)大的值。
实现一个二叉搜索树
- 构造一个节点的类用来存储节点值和左右节点
- 构造一个二叉搜索树的类,它有一个根节点
实现插入节点的方法(insert)
- 根据插入的值创建一个节点
- 判断是否存在根节点
- 不存在根节点:直接将根节点指向此节点
- 存在根节点:将根节点和此节点传入
insertNode方法去处理插入的位置
实现判断插入节点位置的方法(insertNode)。第一个参数为父节点,第二个参数为子节点
- 判断子节点要插入到父节点的左侧还是右侧:比父节点小的插入到父节点左侧,比父节点大的插入到父节点右侧
- 找到子节点要插入到父节点的位置,判断该位置是否已存在
- 如果被插入的位置已存在的,则递归调用
insertNode方法,将父节点替换为被插入位置的节点 - 如果被插入的位置不存在的,直接将子节点插入到父节点上
class Node { // {1}
constructor(value) {
this.val = value; // 节点值
this.left = null; // 左节点
this.right = null; // 右节点
}
}
class BinarySearchTree { // {2}
constructor() {
this.root = null; // 根节点
}
insert(value) {
const node = new Node(value); // {3}
if (this.root === null) { // {4}
this.root = node; // {5}
} else {
this.insertNode(this.root, node); // {6}
}
}
insertNode(root, node) {
if (node.val > root.val) { // {7}
if (root.right !== null) { // {8}
this.insertNode(root.right, node); // {9}
} else {
root.right = node; // {10}
}
} else {
if (root.left !== null) { // {8}
this.insertNode(root.left, node); // {9}
} else {
root.left = node; // {10}
}
}
}
}